52 Kettlebell Exercises for Men and Women

52 Kettlebell Exercises
There are lots of different kettlebell exercises that you can perform, some are more challenging than others.
You will find that there is a natural progression when it comes to training with certain kettle bell exercises so it is important to start at the beginning.
If you decide to jump to the more advanced kb exercises without building up your fundamental skills first then your technique and kettlebell moves will suffer and there is a high chance of injury.
All of the kettlebell movements listed below are single kettlebell exercises but many can be performed as double kettlebell lifts too.
List of Kettlebell Exercises
Here is a list of exercises with a kettlebell starting with the fundamental and most important at the top. Become skilled and proficient in each kettlebell exercise using proper form before moving on to the next. You can thank me for this later 🙂
Kettlebell Slingshot

The kettlebell slingshot is a simple but powerful drill. It builds core control, grip strength, and shoulder stability. You pass the kettlebell around your waist in a smooth, controlled motion. The movement looks easy, but it challenges your balance, coordination, and posture.
This exercise improves anti-rotational strength and teaches your body to stay braced while your arms move freely. It also boosts body awareness, which helps with more advanced exercises like the kettlebell clean and snatch.
A common mistake is twisting the torso instead of staying still. Another is dropping the hands too low or rushing the movement. Focus on staying tall, keeping your core tight, and moving with control. Every rep should feel smooth and deliberate.
Coaching tip: Use the slingshot between heavy sets to stay active without fatiguing. For more of a challenge, combine it with a squat or a reverse lunge.
The slingshot works the shoulders, forearms, obliques, and deep core muscles. It’s a great fit for warm-ups, light conditioning, or active recovery.
Kettlebell Halo

The kettlebell halo is a great mobility and strength drill for the upper body. You rotate the kettlebell around your head in a tight, controlled circle. It opens the shoulders, activates the upper back, and improves neck and thoracic spine mobility.
This exercise builds strength in the delts, traps, and rotator cuff while training you to stay stable and braced. It’s perfect for preparing the body before pressing or overhead work. The halo also reinforces shoulder control in all directions, not just straight lines.
One common mistake is leaning the head forward or moving too fast. Another is letting the elbows flare or the kettlebell drift too far from the neck. Keep your chest tall, your elbows in, and your hands close to the base of your skull.
Coaching tip: Start light and move slowly. Breathe through the movement and stay relaxed in the neck and shoulders. To increase the challenge, add a lunge, kneeling position, or combine it with other flows.
The kettlebell halo trains the shoulders, arms, traps, and upper core. It works well as part of your warm-up or as a recovery movement between heavier sets. Use it regularly to keep your shoulders mobile, strong, and injury-resistant.
Kettlebell Good Morning

The kettlebell good morning is a powerful hinge exercise. It strengthens the hamstrings, glutes, and lower back. The movement teaches proper hip mechanics and improves posture under load. You hold the kettlebell in a racked or goblet position, then hinge at the hips while keeping your spine neutral.
This drill reinforces the same movement pattern used in deadlifts, swings, and cleans. It helps you build control and strength through the posterior chain without using heavy weight. It also develops core stability and spinal awareness.
Many people make the mistake of rounding their back or bending their knees too much. Another issue is letting the kettlebell pull them forward. Keep your knees soft, chest lifted, and hips pushing back. Your spine should stay long and neutral throughout the movement.
Coaching tip: Start with a light kettlebell and focus on form. Go slow and feel the stretch in your hamstrings. For more challenge, try it in a double kettlebell racked position or standing on a low platform for increased range.
The kettlebell good morning trains the posterior chain, spinal stabilizers, and deep core muscles. Use it in warm-ups, mobility flows, or as part of a strength circuit. It’s a smart addition to any program focused on hip power, posture, and injury prevention.
Kettlebell Overhead Warm Up

The kettlebell overhead warm-up is a full-body prep drill. It builds shoulder stability, core engagement, and postural control. You hold a light kettlebell overhead while moving through controlled patterns like carries, marches, or rotations.
This movement wakes up the rotator cuff, traps, and mid-back. It also trains your body to brace the core while the arm stays locked out. That’s essential for any overhead kettlebell work like the press, snatch, or get-up.
Mistakes often include flaring the ribs, shrugging the shoulder, or leaning back. Keep your ribs down, core tight, and shoulder packed. The arm should stay vertical and close to the ear at all times.
Coaching tip: Use a light bell and move with intention. Try pairing it with bird dogs, windmills, or marching for even more control and coordination. You’ll notice better alignment and shoulder endurance almost immediately.
The kettlebell overhead warm-up targets the shoulders, core, lats, and spinal stabilizers. It fits perfectly before any overhead work or as part of a dynamic warm-up. Do it regularly to stay mobile, strong, and pain-free in the shoulders.
Kettlebell Bottoms Up Clean

The kettlebell bottoms-up clean is a powerful drill for building grip strength, shoulder stability, and movement precision. You clean the kettlebell into a racked position with the bell flipped upside down. This demands focus, tension, and full-body control.
The bottoms-up position forces your grip and stabilizers to work harder. It improves wrist alignment, forearm endurance, and rotator cuff activation. It also helps clean up sloppy technique in standard cleans by punishing poor timing or lazy mechanics.
Common mistakes include crushing the grip too tight, overusing the arm, or letting the bell crash into position. Stay smooth and tight. Use your hips to drive the bell and guide it into place with a relaxed but responsive hand.
Coaching tip: Start with a light kettlebell. Make each rep crisp and clean. If you lose the bell’s balance, reset and go again. For added challenge, try bottoms-up holds or walks to build endurance and control.
The kettlebell bottoms-up clean targets the forearms, shoulders, core, and lats. It’s a great exercise for lifters looking to improve control, clean technique, or build stronger, more stable shoulders. Add it to your skill work or warm-up for smarter training.
Kettlebell Single Arm Deadlift
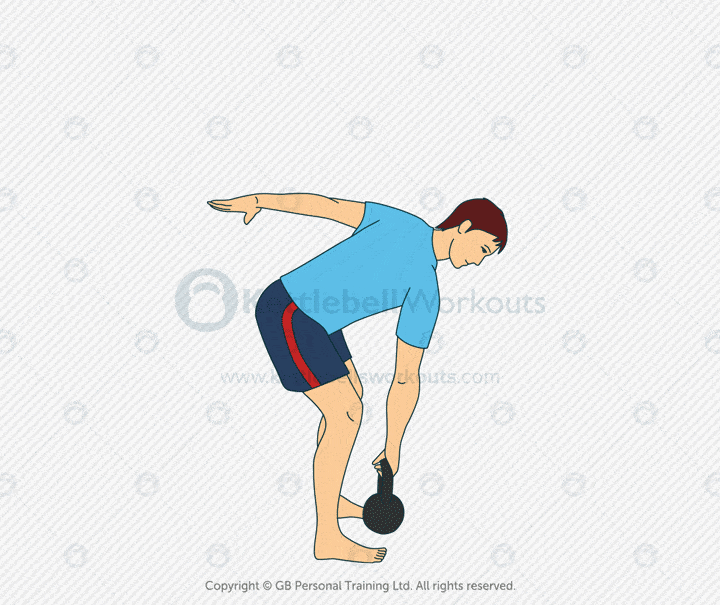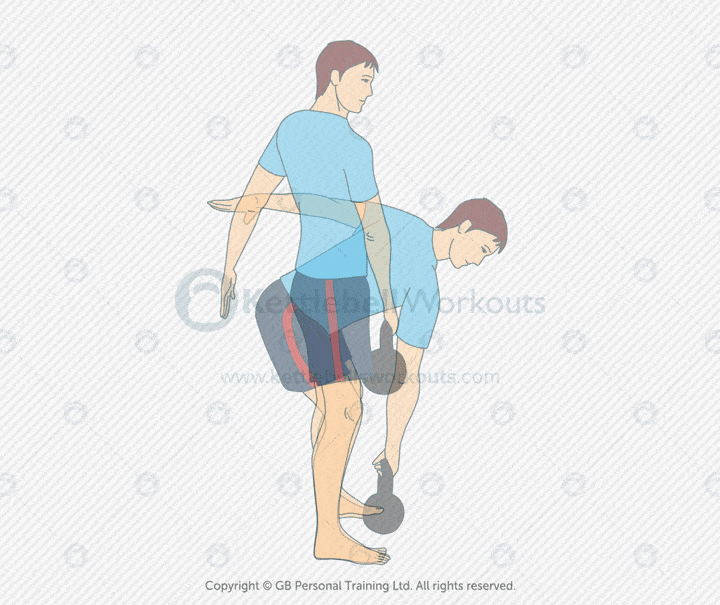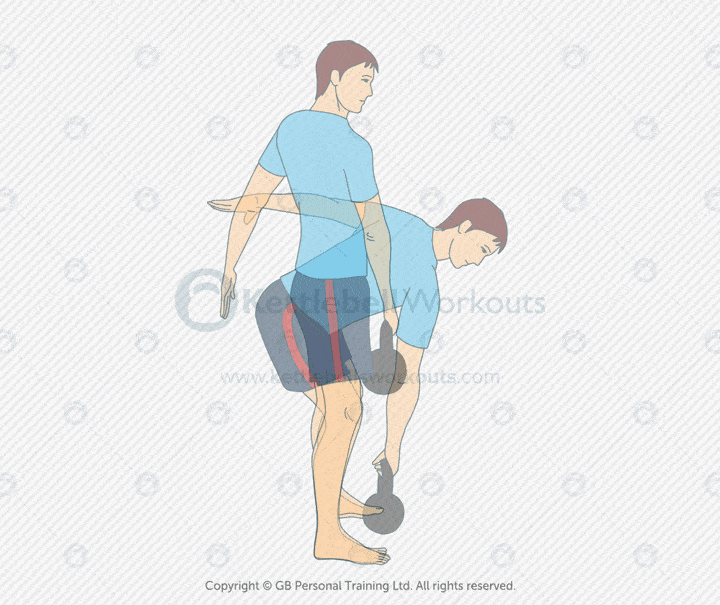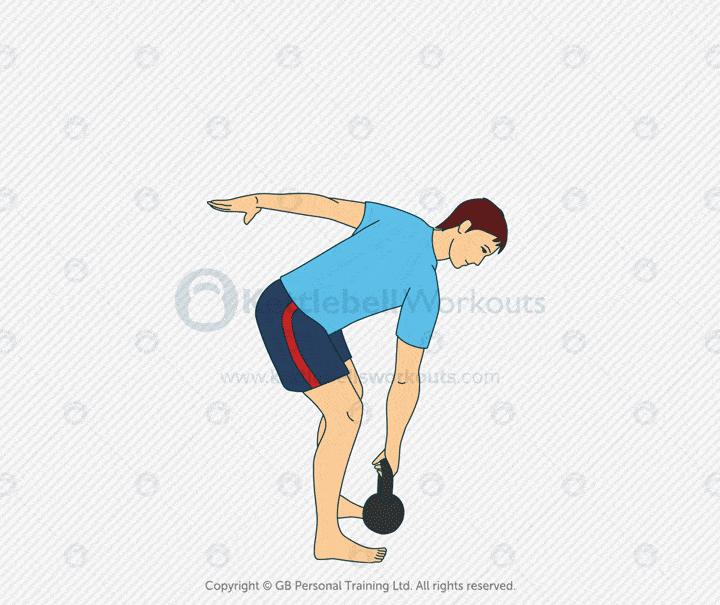
The kettlebell single arm deadlift is a foundational strength movement. It targets the glutes, hamstrings, and lower back while building powerful hip mechanics. Using one arm challenges your ability to stay square and resist rotation.
This variation improves core stability, grip strength, and posterior chain engagement. It also exposes imbalances between sides, helping you build a more symmetrical and resilient body. The movement teaches you to lift with your hips, not your back.
Mistakes include rounding the spine, twisting toward the kettlebell, or squatting the movement. Keep your chest up, hips back, and spine neutral. Your shoulders should stay level throughout the lift.
Coaching tip: Position the kettlebell between your feet. Push through your heels and drive the hips forward to stand. Switch arms each rep or each set to train both sides equally.
The kettlebell single arm deadlift hits the glutes, hamstrings, core, and grip. It’s a smart choice for beginners learning to hinge, or advanced lifters reinforcing technique. Use it in warm-ups, strength circuits, or recovery-focused sessions.
Kettlebell Swing Two Hands
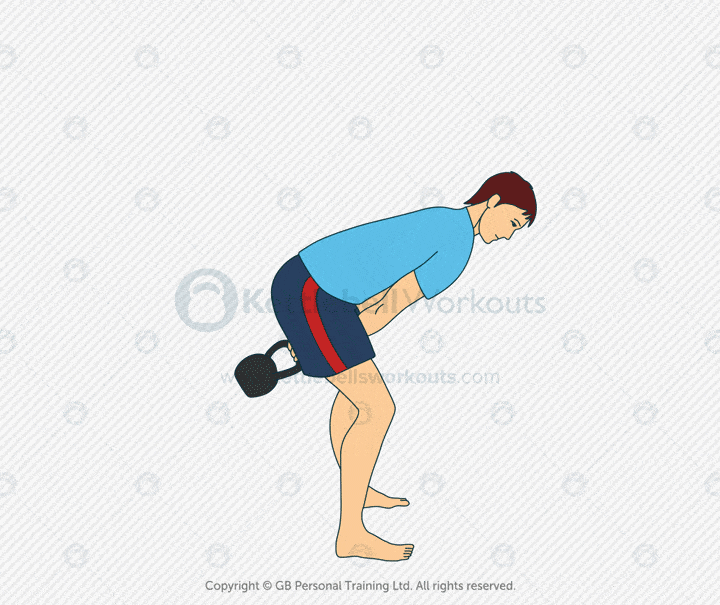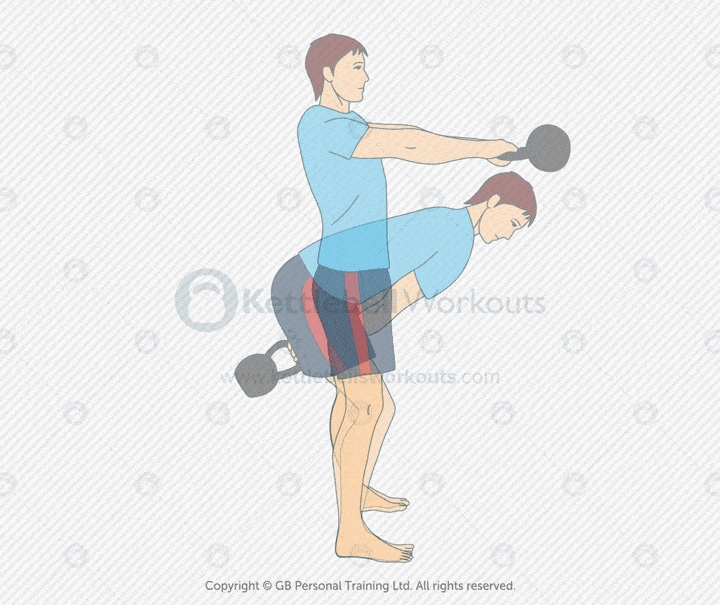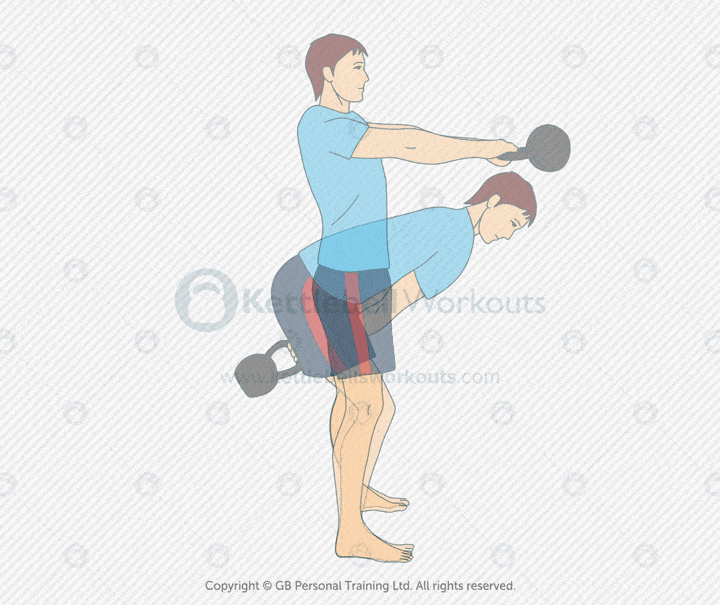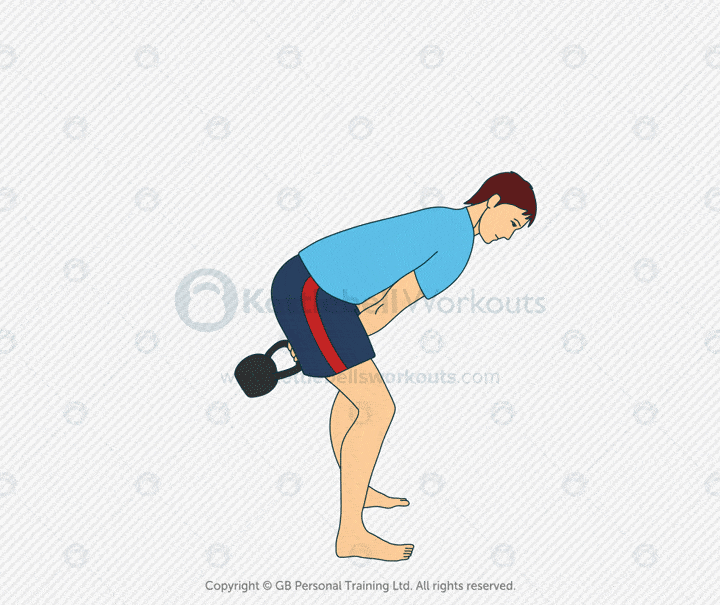
The kettlebell two-handed swing is one of the most effective full-body exercises. It builds explosive hip power, core strength, and cardiovascular conditioning. The swing is a ballistic movement that drives the kettlebell forward using the hips, not the arms.
This movement trains the glutes, hamstrings, lats, and core. It also sharpens coordination and teaches proper hinge mechanics. The result is better posture, faster athletic movement, and increased power for lifts like the deadlift or clean.
Many people make the mistake of squatting instead of hinging. Others lift with their arms or let the kettlebell pull them forward. Keep your feet planted, spine neutral, and arms relaxed. Let the hips snap the bell forward and control the downswing with your lats.
Coaching tip: Hike the kettlebell back between your legs. Keep your arms close to your body. The bell should float at chest height from hip power alone. Start with sets of 10–15 reps and focus on quality over speed.
The two-handed swing works the entire posterior chain, builds core endurance, and improves athletic performance. It’s ideal for conditioning, strength circuits, or as a main lift on lower-body days. Use it often and refine your form over time for maximum results.
Kettlebell Clean
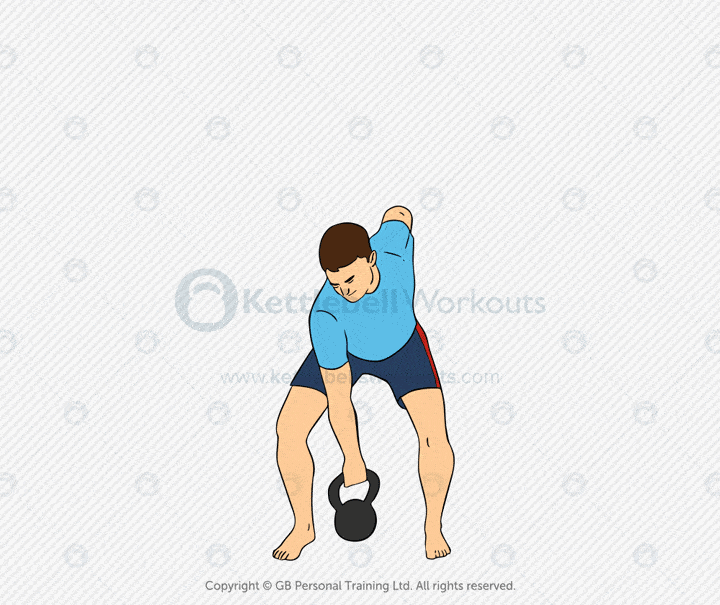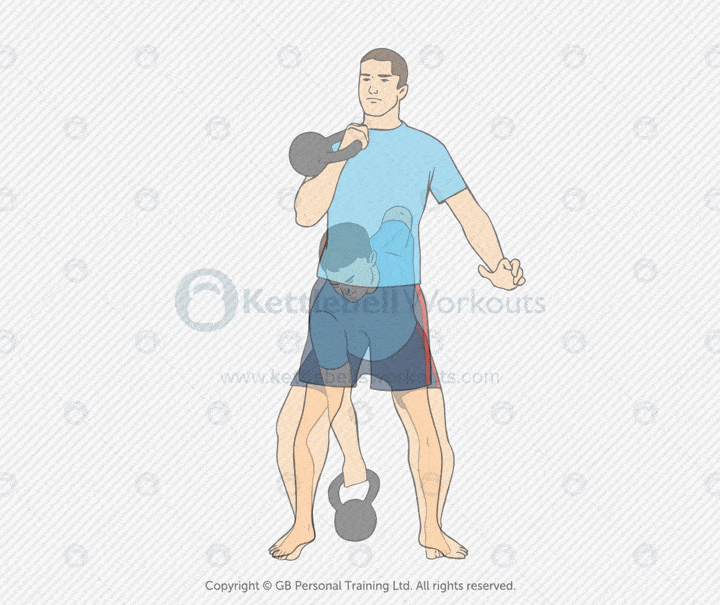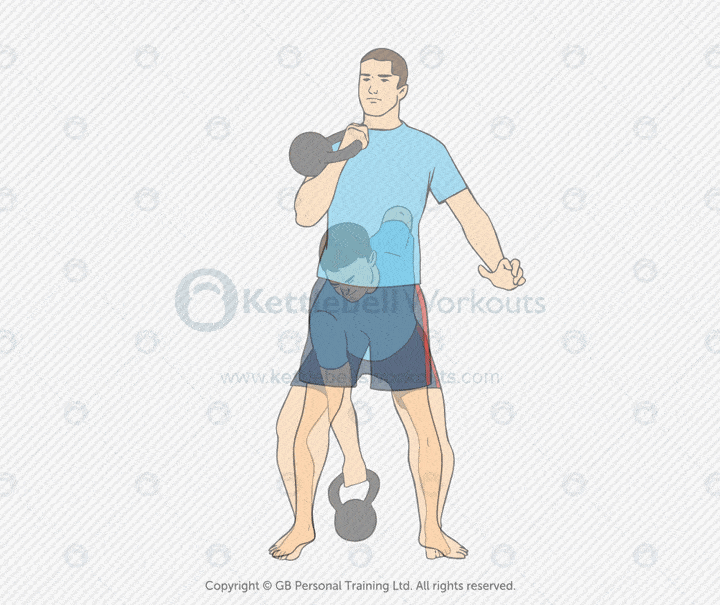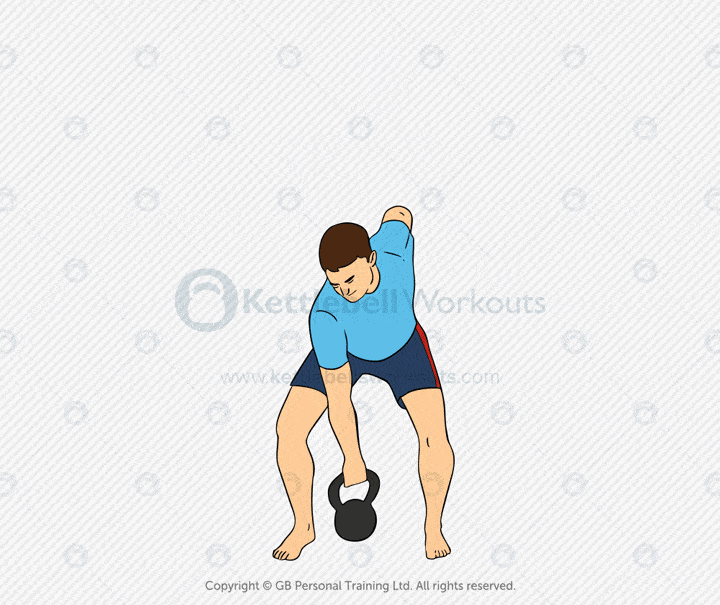
The kettlebell clean is a dynamic strength and skill movement. It brings the kettlebell from the floor or swing into a secure racked position using hip power and timing. It builds explosiveness, coordination, and full-body strength.
This exercise targets the glutes, hamstrings, core, lats, and shoulders. It teaches you how to transfer force from the lower body into a controlled catch. Mastering the clean is key for progressing to the kettlebell press, front squat, or snatch.
Common mistakes include letting the kettlebell crash into the forearm, curling the weight up, or overusing the arms. Keep the bell close to your body. Use your hips to launch it, and guide it softly into position with a loose but precise grip.
Coaching tip: Think of zipping up a jacket—keep the bell close as it travels. Your hand should punch through at the top to catch the bell smoothly. Practice from the dead stop and swing variations to build clean technique.
The kettlebell clean is essential for building efficient power, joint-friendly strength, and smooth movement transitions. Use it as a standalone drill, a warm-up for heavier lifts, or as part of a conditioning circuit.
Kettlebell Single Leg Deadlift

The kettlebell single leg deadlift is a powerful exercise for building balance, hip strength, and posterior chain control. It trains the body to hinge on one leg while staying stable and aligned. This movement challenges your glutes, hamstrings, and core in a way that improves both strength and coordination.
This drill is excellent for identifying and correcting left-to-right imbalances. It also builds ankle stability and teaches you to control rotation and alignment through the hips and spine. It’s especially useful for athletes and anyone working to prevent injury.
Mistakes include rounding the back, reaching with the kettlebell, or losing balance by going too fast. Keep your spine long, your hips level, and your core engaged. Focus on moving through the hips, not the knee or low back.
Coaching tip: Start with a light kettlebell and use a short range of motion until your balance improves. Keep a slight bend in the standing leg and drive the lifted leg back in line with your torso. Control the tempo from start to finish.
The single leg deadlift works the glutes, hamstrings, calves, and deep core muscles. It fits well into warm-ups, strength sessions, or accessory work for runners, lifters, and general fitness. Train both sides evenly for better movement and long-term joint health.
Single-Arm Kettlebell Swing

The kettlebell single-handed swing is a powerful variation of the traditional swing. It builds hip explosiveness, grip strength, and core stability. With one hand on the bell, your body must work harder to stay balanced and resist rotation.
This movement targets the glutes, hamstrings, lats, forearms, and obliques. It also improves timing and coordination, making it a great stepping stone to more advanced drills like the clean or snatch. You’ll feel your core light up as you fight to keep the movement centered.
Mistakes include over-rotating, lifting with the arm, or letting the bell pull you out of alignment. Stay grounded. Let the hips drive the movement. Your arm should act as a guide—not a lifter.
Coaching tip: Keep your non-working hand active. Swing it in sync or place it behind your back to improve balance awareness. Alternate hands every rep or set to train both sides equally.
The single-handed swing trains the entire posterior chain while sharpening anti-rotational control. It’s ideal for developing strength, conditioning, and symmetry. Add it to your sessions when you’re ready to progress from two-handed swings and want more challenge and coordination.
Kettlebell Swing Changing Hands

The kettlebell alternating swing is a dynamic power and coordination drill. It builds explosiveness, timing, and full-body control. You swing the kettlebell with one hand, then switch hands at the top of the arc in mid-air.
This movement trains the glutes, hamstrings, lats, core, and forearms. It also challenges your brain and body to stay in sync. The hand switch demands focus, timing, and grip precision, making it a smart tool for building athletic movement patterns.
Mistakes include switching too low, losing posture, or using the arms instead of the hips. Keep the bell high during the switch. Let the hips drive the power, not your shoulders. Your spine should stay tall and your core engaged at all times.
Coaching tip: Start slow. Get comfortable with the regular single-handed swing first. Time your hand switch at the top when the kettlebell feels weightless. Don’t rush—control leads to better form and safer reps.
The alternating swing improves power output, reaction time, and muscular endurance. It’s perfect for conditioning, athletic circuits, or as a progression from single-handed swings. Use it to add variety and intensity to your kettlebell training.
Kettlebell Side Stepping Swing

The kettlebell side stepping swing is a powerful variation that adds lateral movement to the classic swing. It builds hip power, core stability, and coordination while improving your ability to move dynamically in multiple directions.
This drill targets the glutes, hamstrings, lats, and obliques, while also training the adductors and abductors. Stepping sideways while swinging challenges your body to maintain posture and rhythm under changing foot positions. It’s great for athletes, fighters, and anyone looking to build movement intelligence.
Common mistakes include stepping too wide, losing balance, or twisting the spine. Stay grounded. Keep your hips square and your core braced. The swing should still come from your hips—not your arms or shoulders.
Coaching tip: Start by mastering the two-handed swing. Then add a small lateral step between reps. Step, swing, reset. Keep the footwork light and the movement crisp. This variation is more about timing and control than speed.
The side stepping swing trains power, agility, and lateral coordination. It fits well in strength circuits or as a stand-alone conditioning drill. Add it to your routine to break the straight-line pattern and build next-level athleticism.
Lateral Kettlebell Swing (Kettlebell Side Swing)

The kettlebell lateral swing is an advanced swing variation that builds lateral strength, rotational control, and explosive power. Unlike traditional swings, the kettlebell travels across the body, from one hip to the opposite side, forcing the core and hips to work together to stay aligned.
This movement targets the glutes, hamstrings, obliques, and lats, while also engaging the adductors and hip stabilizers. It improves your ability to generate and control power in a diagonal plane—a key element in sports, martial arts, and functional fitness.
Mistakes often include over-rotating the torso, pulling with the arms, or letting the bell swing too far out. Keep your chest up, hips square, and spine long. Drive the bell with your hips and resist rotation with your core.
Coaching tip: Start light and move slowly at first. Swing the kettlebell from one side of your body to the other, letting it pass just outside the opposite hip. Breathe with each rep and control the rhythm of the swing from your center.
The kettlebell lateral swing builds total-body coordination, anti-rotational strength, and explosive hip drive. Use it as a finisher, a core-focused swing variation, or a functional strength tool to sharpen your athletic movement patterns.
Kettlebell Single Leg Clean

The kettlebell single leg clean is a highly advanced movement that tests balance, coordination, and explosive strength. You clean the kettlebell from the ground or hang while standing on one leg, demanding precise timing and total-body control.
This drill targets the glutes, hamstrings, core, and shoulders, while also challenging the ankles and hip stabilizers. It forces the body to stay aligned and centered while generating power through a single-leg hinge—ideal for athletes and injury prevention.
Common errors include losing balance, twisting during the clean, or letting the bell crash into the rack. Focus on a strong hinge, soft landing, and smooth transition. Keep your eyes fixed on a point in front of you to stay stable.
Coaching tip: Master the standard single leg deadlift and clean first. Then combine them with a light kettlebell. Start slow and prioritize control. As you improve, add speed and weight cautiously.
The kettlebell single leg clean is perfect for improving unilateral power, postural stability, and movement precision. Use it in strength circuits, athletic training blocks, or to add serious skill to your clean progression.
Learn more: Challenge your balance and coordination with the kettlebell single-leg clean.
Kettlebell Snatch

The kettlebell snatch is one of the most powerful and technical kettlebell movements. It builds explosive hip drive, overhead strength, and full-body coordination. You swing the kettlebell from the ground or between the legs straight into an overhead lockout in one smooth motion.
This exercise targets the glutes, hamstrings, core, shoulders, and lats. It improves power, timing, and endurance—making it a top choice for both strength and conditioning. The snatch also demands excellent mobility and control, especially at the shoulder and thoracic spine.
Common mistakes include yanking the bell with the arm, letting it flop over the wrist, or finishing with a loose overhead position. Use your hips to generate force. Keep the bell close to your body and “punch through” at the top for a smooth lockout.
Coaching tip: Break it down by first mastering the swing, high pull, and press. Then combine them into a seamless snatch. Start with low reps and light weight to perfect your form before building volume or intensity.
The kettlebell snatch is ideal for building explosive strength, cardio capacity, and overhead control. Use it as a peak lift in your training, or incorporate it into circuits for high-intensity conditioning.
Kettlebell Goblet Squat

The kettlebell goblet squat is one of the best foundational strength exercises. It builds leg strength, core stability, and postural control. Holding the kettlebell at chest level helps keep the torso upright and reinforces proper squat mechanics.
This movement targets the quads, glutes, hamstrings, and core. It also improves mobility in the hips, ankles, and thoracic spine. The goblet squat is ideal for teaching beginners how to squat with good form and for seasoned lifters as a powerful accessory lift.
Common mistakes include letting the chest drop, collapsing the knees inward, or holding the kettlebell too low. Keep your elbows tight, chest proud, and drive through your heels to stand tall.
Coaching tip: Hold the kettlebell close to your sternum. Sink down between your hips, not forward. Pause at the bottom to feel the tension, then drive up with power. Breathe steadily and stay tight through your core.
The kettlebell goblet squat develops lower body strength, trunk control, and movement quality. Use it in warm-ups, strength circuits, or as a volume-builder to improve squat depth and endurance.
Kettlebell Racked Squat

The kettlebell racked squat is a powerful lower-body strength exercise that also trains core engagement, postural stability, and shoulder endurance. Holding the kettlebell in the racked position shifts the center of gravity and challenges the body to stay upright throughout the squat.
This movement targets the quads, glutes, hamstrings, and core, while also engaging the upper back and obliques. It’s excellent for building single-side strength when done unilaterally, or full-body strength when using two kettlebells.
Common mistakes include letting the kettlebell drift forward, collapsing the torso, or losing tension in the bottom position. Keep your elbow close to your ribs, wrist neutral, and core braced. Your squat should be smooth, deep, and controlled.
Coaching tip: Start with a light kettlebell to master the rack position. Squat down with control, keeping the weight balanced and your chest lifted. For added intensity, try double racked squats or add a pause at the bottom to increase time under tension.
The kettlebell racked squat is a go-to movement for developing leg strength, core resilience, and postural alignment. Use it as a main lift or accessory exercise to build strength and control across multiple planes.
Kettlebell Racked Reverse Lunge

The kettlebell racked reverse lunge is a powerful unilateral exercise that builds leg strength, core stability, and postural control. Holding the kettlebell in the racked position forces the body to stay tall and engaged while the lower body moves through a deep lunge pattern.
This movement targets the quads, glutes, hamstrings, and core, while also challenging the shoulders, obliques, and hip stabilizers. It helps correct imbalances, improves single-leg strength, and enhances coordination.
Mistakes often include leaning forward, losing balance, or letting the kettlebell sag in the rack. Keep your torso upright, your core tight, and your elbow close to your ribs. Step back with control and push through the front heel to return to standing.
Coaching tip: Start with a light kettlebell in the rack. Step back slowly and focus on stability over depth. You can alternate legs or stay on one side to increase the training load on a specific leg. For a challenge, try double racked lunges or walking variations.
The kettlebell racked reverse lunge develops unilateral strength, balance, and midline control. It’s perfect as a main lift, accessory movement, or part of a full-body circuit focused on real-world strength and movement.
Kettlebell Bob and Weave

The kettlebell bob and weave is a dynamic movement that builds lateral agility, leg strength, and core activation. It mimics the defensive motion seen in boxing—dipping under an imaginary punch while staying low and controlled.
This exercise targets the quads, glutes, inner thighs, and obliques. Holding a kettlebell adds resistance that challenges your posture and balance as you shift from side to side. It’s excellent for improving coordination and real-world mobility.
Common mistakes include rounding the back, rising up too high, or letting the kettlebell pull you forward. Keep your spine long, chest up, and feet grounded. Move with control from one side to the other, maintaining tension throughout.
Coaching tip: Hold the kettlebell at chest height in a goblet position. Sink into a quarter squat and move laterally in a smooth arc. Imagine ducking under a rope or a punch. The movement should feel fluid, not rushed.
The kettlebell bob and weave enhances lateral movement, postural endurance, and core stability. Use it in warm-ups, agility circuits, or as a conditioning drill that builds athletic control and resilience.
Learn more: Add lateral movement to your training with the kettlebell bob and weave.
Kettlebell Tactical Lunge

The kettlebell tactical lunge is a functional strength and coordination exercise. It combines a reverse lunge with a kettlebell hand-off underneath the front leg. This added element improves balance, hip mobility, and core control.
The movement targets the quads, glutes, hamstrings, adductors, and core, while also demanding focus and timing. Passing the kettlebell under the leg forces your stabilizers to engage and teaches you how to move with precision under load.
Common mistakes include twisting the torso, rushing the pass, or letting the front knee cave in. Keep your chest tall, core tight, and move deliberately. The kettlebell should pass smoothly from one hand to the other without breaking form.
Coaching tip: Start with bodyweight or a light kettlebell to learn the rhythm. Step back into a lunge, pass the kettlebell under the front leg, and return to standing. Alternate sides with each rep for balanced development.
The kettlebell tactical lunge builds functional lower-body strength, dynamic stability, and movement coordination. It fits perfectly in conditioning workouts, agility circuits, or mobility-focused sessions for total-body control.
Learn more: Try the kettlebell tactical lunge to combine lower body strength with core control.
Kettlebell Lunge with Rotation

The kettlebell lunge with rotation is a dynamic movement that combines lower-body strength with core engagement and rotational control. As you step into a lunge, you rotate the kettlebell across your body, challenging your balance and coordination.
This exercise targets the quads, glutes, hamstrings, obliques, and deep core muscles. The rotational element trains your torso to stay stable under movement, improving functional strength for sports, daily life, and injury prevention.
Common mistakes include twisting through the knees, letting the torso collapse, or rushing the movement. Keep your chest tall, spine neutral, and rotate from the midsection—not the shoulders or hips. The movement should feel strong and deliberate.
Coaching tip: Hold the kettlebell in front of your chest in a goblet grip. Step into a lunge, rotate over the front leg, then return to centre as you stand. Start slow and controlled to master your balance and form.
The kettlebell lunge with rotation builds rotational strength, postural stability, and movement coordination. Use it in mobility circuits, strength sessions, or core-focused workouts to add a new dimension of control and power to your training.
Kettlebell Double Lunge

The kettlebell double lunge is a high-impact unilateral exercise that builds lower-body strength, coordination, and muscular endurance. It combines a forward lunge and a reverse lunge on the same leg, demanding full control and balance under load.
This movement targets the quads, glutes, hamstrings, calves, and core. The continuous motion increases time under tension, helping to build strength and stability in each leg individually. It also improves joint control and builds resilience in the knees and hips.
Common mistakes include leaning forward, rushing the transitions, or allowing the kettlebell to shift off-center. Keep your torso upright, core tight, and steps deliberate. Move with control from front to back and stay grounded through your whole foot.
Coaching tip: Hold the kettlebell in a goblet or racked position. Step forward into a lunge, return to center, then step back into a reverse lunge. Keep the same leg working through both phases before switching sides.
The kettlebell double lunge enhances single-leg strength, postural alignment, and overall conditioning. Use it as a challenging strength accessory, a balance builder, or part of a conditioning circuit that pushes both body and mind.
Kettlebell Side Lunge

The kettlebell side lunge is a powerful lower-body exercise that develops lateral strength, hip mobility, and core stability. It shifts your movement out of the traditional forward-backward plane and into the side-to-side pattern most people neglect.
This exercise targets the glutes, quads, inner thighs, hamstrings, and obliques. Stepping laterally builds strong, mobile hips and improves control through a wide range of motion. It’s excellent for athletes, functional training, and injury prevention.
Common mistakes include leaning forward, collapsing the knee inward, or shifting the kettlebell off-center. Keep your chest up, spine neutral, and step out with purpose. Sink into the hip while keeping the opposite leg straight.
Coaching tip: Hold the kettlebell in a goblet or racked position. Step out to the side, load the working hip, and push back to center with control. Move slowly at first and stay balanced throughout the motion.
The kettlebell side lunge builds unilateral strength, hip stability, and lateral coordination. It’s a smart addition to any leg workout, mobility session, or full-body training plan that prioritizes real-world movement and injury resistance.
Kettlebell Overhead Squat

The kettlebell overhead squat is a highly advanced movement that builds full-body strength, mobility, and stability. Holding the kettlebell overhead challenges your ability to stay upright and maintain balance while moving through a deep squat.
This exercise targets the quads, glutes, hamstrings, core, shoulders, and upper back. It demands exceptional mobility in the ankles, hips, thoracic spine, and shoulders, making it both a strength builder and a diagnostic tool for movement quality.
Common mistakes include losing the overhead position, allowing the knees to collapse, or leaning forward excessively. Keep the kettlebell stacked over your shoulder, ribs down, and core braced. Move slowly and stay controlled from top to bottom.
Coaching tip: Start with a light kettlebell and use a single-arm position. Focus on maintaining vertical alignment through the arm, spine, and hips. Pause in the bottom position to work on depth and control before standing tall.
The kettlebell overhead squat develops postural strength, shoulder stability, and joint mobility. Use it as a movement screen, a mobility drill, or an advanced strength challenge for experienced kettlebell lifters.
Learn more: Improve shoulder mobility and total-body strength with the kettlebell overhead squat.
Kettlebell Overhead Reverse Lunge

The kettlebell overhead reverse lunge is a demanding full-body exercise that combines leg strength, shoulder stability, and core control. Holding the kettlebell overhead forces your body to stay tall and engaged while stepping backward into a deep lunge.
This movement targets the quads, glutes, hamstrings, obliques, and shoulders, while also challenging balance and mobility. It improves stability in the overhead position and reinforces strong posture throughout dynamic movement.
Common mistakes include arching the lower back, losing the overhead lockout, or rushing the step back. Keep your ribs down, arm vertical, and core braced. Move with control and precision through every rep.
Coaching tip: Start with a light kettlebell in a strong overhead position. Step back into a reverse lunge while keeping the kettlebell steady above your shoulder. Focus on balance and breathing to stay centered.
The kettlebell overhead reverse lunge builds unilateral strength, rotational control, and shoulder endurance. Use it as part of a mobility-focused session, a strength circuit, or to challenge advanced movement patterns.
Learn more: Build stability and postural control with the kettlebell overhead reverse lunge.
Kettlebell Overhead Walking Lunge

The kettlebell overhead walking lunge is an advanced strength and stability exercise. It combines unilateral leg work with a loaded overhead position, challenging your entire body to move with precision, control, and balance.
This movement targets the quads, glutes, hamstrings, core, and shoulders. Walking lunges already demand coordination and leg strength, but the overhead kettlebell increases the demand on your postural control, shoulder endurance, and anti-rotational stability.
Common mistakes include leaning forward, wobbling in the overhead position, or arching the lower back. Keep your arm locked out, ribs down, and torso upright. Each step should be steady and deliberate.
Coaching tip: Start with a light kettlebell and focus on maintaining a strong, vertical arm throughout. Step into each lunge slowly, making sure the back knee lowers with control. Stay tall and centered from start to finish.
The kettlebell overhead walking lunge builds functional strength, joint stability, and real-world movement control. It’s a great choice for advanced lifters, athletes, or anyone looking to challenge their body in new, meaningful ways.
Kettlebell Side Lunge and Clean

The kettlebell side lunge and clean is a dynamic combination movement that builds lateral strength, hip mobility, and explosive power. It blends a deep side lunge with a kettlebell clean, challenging coordination and control across multiple planes.
This exercise targets the glutes, quads, inner thighs, hamstrings, core, and shoulders. The side lunge develops mobility and stability in the hips, while the clean reinforces powerful hip extension and crisp timing.
Common mistakes include rushing the clean, twisting the spine, or collapsing into the lunge. Step wide with control, sink into your hip, and keep your spine tall. As you rise, use your hips to clean the kettlebell smoothly into the rack.
Coaching tip: Hold the kettlebell in one hand and initiate a lateral step into a deep lunge. As you drive back to center, clean the kettlebell into the rack position in one fluid motion. Focus on clean transitions and even pacing.
The kettlebell side lunge and clean builds multi-directional strength, movement precision, and athletic coordination. Use it in strength flows, functional circuits, or as a powerful accessory lift to sharpen total-body control.
Kettlebell Pistol Squat

The kettlebell pistol squat is a highly advanced single-leg exercise that develops leg strength, balance, and mobility. Performing a deep squat on one leg while holding a kettlebell requires total body control and exceptional lower-body coordination.
This movement targets the quads, glutes, hamstrings, calves, and core, while also challenging ankle mobility and hip stability. Holding a kettlebell in front helps counterbalance the movement and improves focus through the descent.
Common mistakes include collapsing forward, lifting the heel, or rushing the motion. Keep your chest up, core tight, and move slowly. Lower with control, pause at the bottom, and drive through your heel to return to standing.
Coaching tip: Use a light kettlebell in a goblet position for balance. If full depth is challenging, start by lowering onto a box or using support. Over time, work toward a full-range pistol with clean form and steady pacing.
The kettlebell pistol squat builds unilateral strength, mobility, and body control. It’s an elite-level movement perfect for advanced training, mobility progressions, and mastering real-world leg power.
Kettlebell Bent-Over Row

The kettlebell bent-over row is a fundamental pulling exercise that builds upper-back strength, grip endurance, and core stability. It involves rowing the kettlebell toward your torso while maintaining a strong, hinged position.
This movement targets the lats, rhomboids, rear delts, biceps, and core. It also reinforces postural strength by training you to stabilize the spine under load. The bent-over row is key for balancing out push-heavy programs and supporting healthy shoulders.
Common mistakes include rounding the back, shrugging the shoulder, or using momentum to yank the bell. Keep your spine neutral, shoulder packed, and elbow close to your body. Pull with control and lower with purpose.
Coaching tip: Hinge at the hips and rest one hand on a bench, your knee, or use a split-stance for balance. Row the kettlebell in a straight line toward your hip. Pause briefly at the top to squeeze your back before lowering.
The kettlebell regular row develops upper-body pulling strength, postural alignment, and scapular control. It’s a staple for balanced strength training and should be a regular part of any kettlebell routine.
Kettlebell Suitcase Row Exercise

The kettlebell suitcase row is a unilateral pulling movement that builds back strength, core stability, and grip control. Performed in a standing or split stance, this variation mimics the motion of picking up a suitcase, training your body to resist rotation while pulling with power.
This exercise targets the lats, rhomboids, rear delts, biceps, and obliques. Unlike a traditional row, the suitcase setup increases the demand on the anti-rotational core muscles, helping to improve functional strength and postural control.
Common mistakes include twisting the torso, letting the shoulder roll forward, or jerking the kettlebell. Focus on keeping your spine straight, shoulder packed, and core tight. The pull should be strong but controlled, with a clean line from the bell to your ribs.
Coaching tip: Use a split stance or slight hinge. Keep the kettlebell close to your side and row by pulling your elbow back in line with your body. Pause at the top, squeeze your back, and lower under control.
The kettlebell suitcase row builds unilateral pulling power, spinal stability, and rotational control. It’s perfect for balancing push work, improving posture, and developing real-world strength for lifting, carrying, and bracing.
Kettlebell Renegade Row

The kettlebell renegade row is a powerful total-body exercise that combines core stability, upper-body strength, and anti-rotational control. Performed from a plank position, it challenges your body to stay braced while rowing one kettlebell at a time.
This movement targets the lats, rhomboids, triceps, shoulders, and obliques. Holding a solid plank while performing the row also activates the glutes, quads, and deep core muscles, making it a full-body effort.
Common mistakes include letting the hips sag or twist, shrugging the shoulders, or rushing the row. Keep your feet wide for balance, core tight, and hips level. The body should stay as still as possible while the arm moves.
Coaching tip: Set up with two kettlebells directly under your shoulders. Row one kettlebell by pulling the elbow back, keeping the bell close to your side. Pause briefly, lower with control, and alternate sides. Focus on minimal movement through the torso.
The kettlebell renegade row builds pulling strength, postural endurance, and rotational stability. It’s perfect for strength circuits, functional training, or any workout focused on full-body control and resilience.
Kettlebell High Pulls
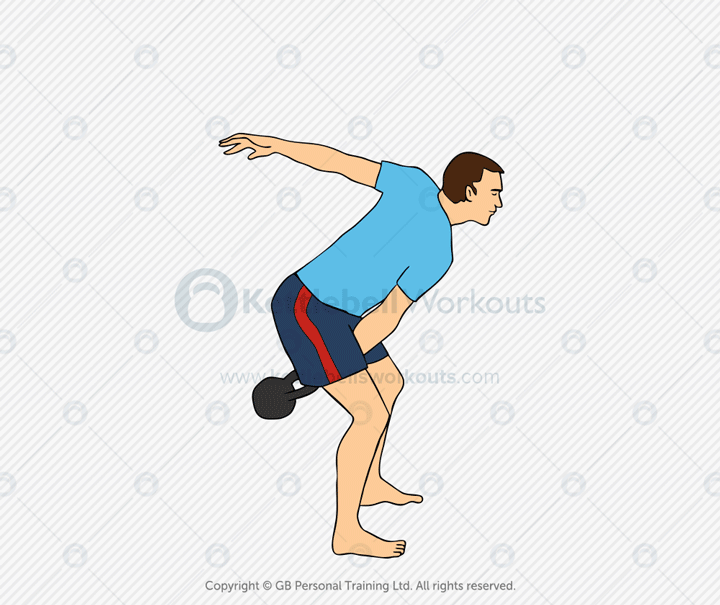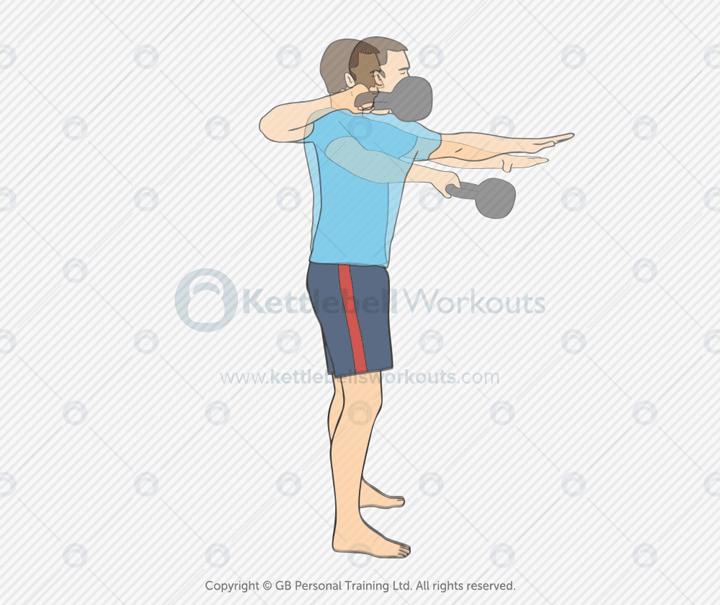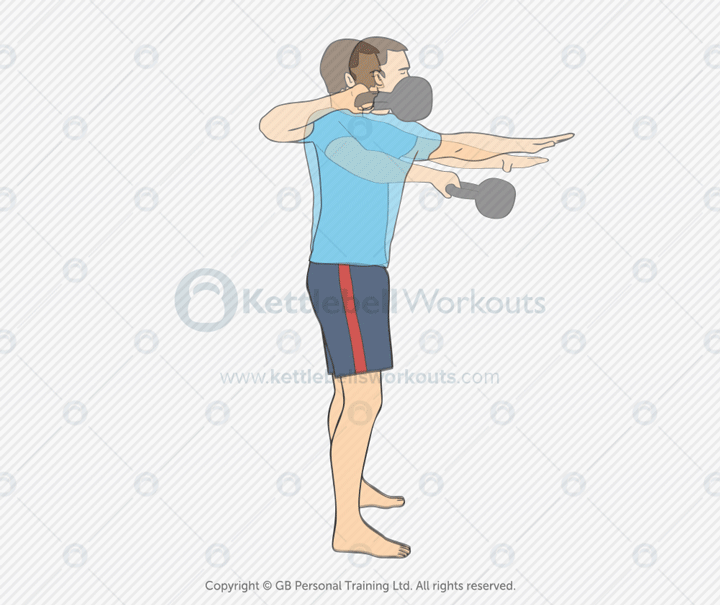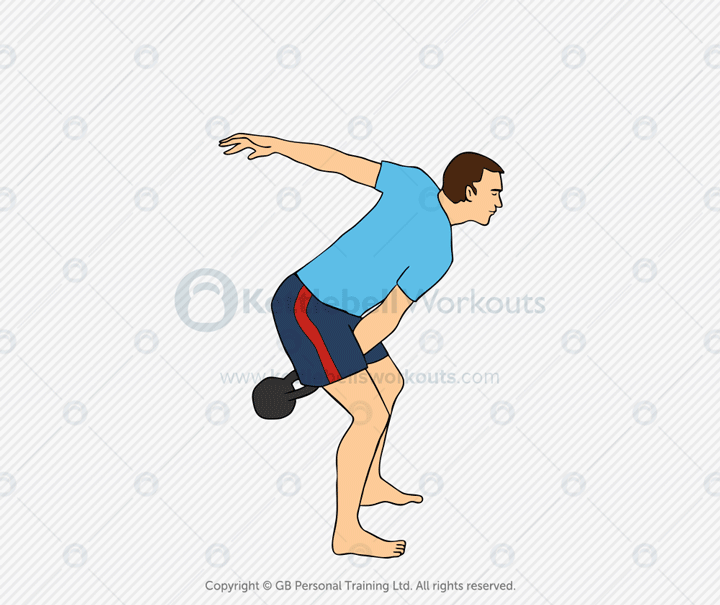
The kettlebell high pull is an explosive pulling exercise that builds upper-body power, hip drive, and coordination. It’s performed by snapping the kettlebell up from the hips and pulling it toward the upper chest with the elbow leading the motion.
This movement targets the glutes, hamstrings, lats, traps, rear delts, and biceps. The high pull serves as a transitional drill between the swing and snatch, helping to sharpen timing, mechanics, and control through the pull phase.
Common mistakes include overusing the arms, pulling too early, or letting the kettlebell drift too far from the body. Drive through the hips, then guide the bell upward with a high elbow and relaxed grip. The movement should be crisp and fluid.
Coaching tip: Begin with a strong hip snap from the swing. As the kettlebell floats upward, lead the pull with your elbow, keeping the bell close. Pause briefly, then let it fall back into the next swing with control.
The kettlebell high pull builds explosive power, upper-back strength, and movement coordination. It’s an excellent drill for advanced conditioning, skill development, or prepping for more complex ballistic lifts like the snatch.
Kettlebell Overhead Press

The kettlebell overhead press is a foundational strength movement that builds shoulder stability, upper-body strength, and core engagement. Pressing the kettlebell from a racked position to full lockout challenges control through the entire range of motion.
This exercise targets the delts, triceps, traps, lats, and core. The offset load of the kettlebell requires you to stabilize the bell throughout the lift, activating more stabilizer muscles than a traditional barbell press.
Common mistakes include arching the back, flaring the elbow, or pressing out of alignment. Keep your ribs down, glutes engaged, and elbow tucked under the wrist. Press the bell in a straight line overhead with full control.
Coaching tip: Start in a strong racked position. Squeeze your glutes and brace your core as you press. At the top, the arm should be vertical with the bicep near your ear. Lower slowly back to the rack to complete the rep.
The kettlebell overhead press develops vertical pushing strength, shoulder health, and postural control. Use it as a main lift, accessory movement, or within full-body kettlebell complexes for strength and endurance.
Kettlebell Squat and Press

The kettlebell squat and press is a powerful full-body movement that combines a front squat with an overhead press. It builds explosive strength, endurance, and coordination, making it ideal for conditioning and strength circuits.
This exercise targets the quads, glutes, hamstrings, core, shoulders, and triceps. By linking the squat and press into one fluid motion, you train your body to generate force from the lower body and transfer it through the upper body efficiently.
Common mistakes include rushing the transition, arching the back during the press, or letting the knees collapse in the squat. Keep your chest tall, knees tracking over your toes, and press the kettlebell directly overhead with full lockout.
Coaching tip: Hold the kettlebell by the horns at chest height. Squat deep, then explode upward and press the kettlebell overhead in one motion. Use the power from your legs to drive the bell, not just your arms.
The kettlebell squat and press develops total-body power, metabolic conditioning, and functional movement patterns. It’s perfect for high-rep workouts, finishers, or full-body kettlebell training sessions.
Kettlebell Push Press

The kettlebell push press is an explosive overhead movement that blends lower-body power with upper-body strength. By using a small dip and drive from the legs, you launch the kettlebell overhead with more force than a strict press allows.
This exercise targets the quads, glutes, core, shoulders, triceps, and traps. The leg drive adds intensity and makes it possible to move heavier loads or push through fatigue while still reinforcing solid pressing mechanics.
Common mistakes include dipping too low, pressing too early, or losing alignment in the overhead position. Keep your dip short and vertical, explode through the hips, and finish with the arm locked out and the bell stacked over your shoulder.
Coaching tip: Start in a strong racked position. Dip quickly by bending the knees, then drive up and press the bell overhead in one fluid motion. Control the kettlebell back to the rack position and repeat with rhythm and focus.
The kettlebell push press develops athletic power, shoulder endurance, and full-body coordination. Use it in strength blocks, interval circuits, or kettlebell complexes for a fast, efficient way to build overhead capacity.
Kettlebell Tall Kneeling Press

The kettlebell tall kneeling press is a strict upper-body strength movement that emphasizes core stability, hip alignment, and shoulder control. Performed from a tall kneeling position, it eliminates lower-body assistance, forcing the upper body to do all the work.
This exercise targets the delts, triceps, upper back, and deep core muscles. The kneeling stance also activates the glutes and requires spinal alignment, making it an excellent drill for reinforcing good posture and pressing mechanics.
Common mistakes include arching the lower back, flaring the ribcage, or leaning to one side. Keep your hips stacked under your shoulders, glutes engaged, and core braced throughout the movement.
Coaching tip: Begin in a tall kneeling position with both knees down and hips extended. Press the kettlebell overhead smoothly, keeping the arm close to your head. Lock out with control, then lower back to the racked position with full tension.
The kettlebell tall kneeling press builds pure overhead strength, postural awareness, and midline stability. It’s perfect for refining technique, correcting asymmetries, or strengthening the upper body without involving momentum.
Kettlebell Half Kneeling Press

The kettlebell half kneeling press is a unilateral strength exercise that enhances shoulder stability, core control, and hip alignment. With one knee down and the opposite foot forward, this position challenges balance while isolating the pressing arm.
This movement targets the delts, triceps, traps, and obliques, while also engaging the glutes and hip flexors. The staggered base makes it easier to identify and correct side-to-side imbalances in strength or mobility.
Common mistakes include leaning back, twisting the torso, or letting the kettlebell drift out of line. Keep your core tight, glutes engaged, and press the bell in a straight vertical path over your shoulder.
Coaching tip: Set up with your front knee at 90 degrees and back foot flat or toes tucked. Hold the kettlebell in the racked position on the same side as your back leg. Press straight up, keeping your body tall and aligned.
The kettlebell half kneeling press improves overhead pressing mechanics, unilateral strength, and rotational control. It’s ideal for warm-ups, movement prep, or focused strength work that reinforces quality and balance.
Kettlebell Thruster

The kettlebell thruster is a powerful, full-body movement that combines a front squat with an overhead press. It’s designed to build explosive strength, muscular endurance, and total-body coordination in one fluid motion.
This exercise targets the quads, glutes, hamstrings, core, shoulders, and triceps. The squat loads the lower body, and the press transfers that power through the upper body—making it a highly efficient movement for strength and conditioning.
Common mistakes include rushing the transition, leaning forward during the squat, or pressing before fully extending the hips. Focus on a smooth flow from the bottom of the squat to the top of the press. Keep the core braced and the kettlebell close to your center.
Coaching tip: Hold the kettlebell in a goblet or racked position. Squat deep with control, then explode up and press the kettlebell overhead in one motion. Lock out fully before returning to the next rep.
The kettlebell thruster is excellent for developing full-body power, cardiovascular conditioning, and movement efficiency. It’s perfect for high-rep circuits, strength-endurance training, or metabolic finishers.
Kettlebell Clean and Press

The kettlebell clean and press is a classic compound movement that builds total-body strength, coordination, and power. It combines a ballistic hip-driven clean with a strict overhead press, demanding both explosive energy and controlled strength.
This exercise targets the glutes, hamstrings, core, lats, shoulders, and triceps. The clean builds hip power and pulling mechanics, while the press reinforces overhead stability and upper-body strength.
Common mistakes include swinging the kettlebell too far from the body, letting it crash into the forearm, or pressing before achieving a solid rack position. Clean the bell with a tight arc, pause briefly, then press with a strong, vertical finish.
Coaching tip: Perform the clean by driving through the hips, guiding the kettlebell into the rack with minimal impact. Brace your core and squeeze your glutes as you press overhead. Lower under control before resetting or linking to the next rep.
The kettlebell clean and press is a go-to lift for developing functional strength, explosive power, and movement efficiency. It fits perfectly into strength circuits, conditioning flows, or as a stand-alone lift for total-body development.
Kettlebell Clean and Push Press
The kettlebell clean and push press is a powerful combination exercise that builds explosive strength, overhead stability, and total-body coordination. It links a hip-driven clean with a leg-assisted press, making it ideal for moving heavier loads efficiently.
This movement targets the glutes, hamstrings, core, lats, delts, and triceps. The clean sets the foundation with a strong hip hinge, while the push press uses leg drive to launch the kettlebell overhead with speed and control.
Common mistakes include cleaning with the arms, pressing too early, or losing alignment at the top. Focus on a clean catch in the rack, a quick and vertical dip, and a strong punch to lockout with the bell stacked over your shoulder.
Coaching tip: Clean the kettlebell into the rack position using your hips, not your arms. Dip slightly by bending your knees, then drive through your legs to press the bell overhead. Keep your core tight and glutes engaged throughout.
The kettlebell clean and push press develops functional power, pressing efficiency, and movement flow. It’s perfect for strength circuits, athletic conditioning, or building endurance under load.
Kettlebell Lunge and Press

The kettlebell lunge and press is a compound movement that combines lower-body strength with upper-body pressing power. By linking a lunge with an overhead press, this exercise trains coordination, balance, and full-body control.
It targets the quads, glutes, hamstrings, core, shoulders, and triceps. The lunge builds unilateral leg strength and stability, while the press adds an overhead challenge that activates the core and upper body.
Common mistakes include rushing the transition, leaning forward, or losing balance during the press. Step into the lunge with control, maintain an upright posture, and press once you’ve stabilized your position.
Coaching tip: Start with the kettlebell in the racked position. Step into a reverse or forward lunge, then press the kettlebell overhead once your balance is secure. Lower with control and return to standing before switching legs.
The kettlebell lunge and press develops functional strength, unilateral coordination, and core-to-extremity power. It’s a perfect addition to strength flows, conditioning circuits, or mobility-focused training days.
Kettlebell Static Lunge and Press

The kettlebell static lunge and press is a controlled, strength-focused movement that builds unilateral leg strength, core stability, and overhead pressing power. Unlike dynamic lunges, the static stance removes momentum, increasing the challenge to your balance and coordination.
This exercise targets the quads, glutes, hamstrings, core, shoulders, and triceps. Holding a lunge position while pressing overhead forces your body to stabilize from the ground up, making it a highly functional movement for athletes and general fitness.
Common mistakes include wobbling through the press, losing alignment, or letting the back knee collapse. Keep your hips square, core tight, and arm vertical as you press.
Coaching tip: Set up in a deep lunge with your front foot flat and your back knee hovering or lightly touching the ground. Hold the kettlebell in a racked position, press overhead with control, and lower back to the rack before switching sides.
The kettlebell static lunge and press enhances isometric control, postural alignment, and total-body strength. It’s ideal for focused strength training, rehab progression, or refining movement under tension.
Kettlebell Clean, Squat and Press

The kettlebell clean, squat, and press is a full-body combination movement that builds strength, coordination, and explosive power. It links three foundational patterns into one fluid sequence—making it ideal for total-body conditioning and movement efficiency.
This exercise targets the glutes, quads, hamstrings, core, shoulders, and triceps. The clean develops hip power, the squat builds lower-body strength and mobility, and the press trains overhead control and upper-body drive.
Common mistakes include letting the kettlebell crash in the clean, losing depth in the squat, or pressing with poor posture. Clean with control, squat with tension, and press in a vertical path while keeping your core tight.
Coaching tip: Start with the kettlebell in one hand. Clean it to the rack, perform a deep front squat, then press the bell overhead as you rise. Focus on clean transitions between each phase of the movement.
The kettlebell clean, squat, and press develops total-body strength, movement fluidity, and functional athleticism. It’s a go-to choice for metabolic conditioning, strength circuits, or complex-based training sessions.
Kettlebell Bottoms Up Press

The kettlebell bottoms-up press is a precision-driven strength movement that improves shoulder stability, grip strength, and core control. Holding the kettlebell upside down increases the demand on your stabilizers throughout the press.
This exercise targets the delts, triceps, forearms, and deep core muscles. Because the bell is inverted, your body must work harder to stay aligned and steady, making it excellent for improving pressing mechanics and joint health.
Common mistakes include rushing the lift, gripping too tightly, or letting the kettlebell drift out of vertical alignment. Focus on a relaxed but responsive grip, a slow and controlled press, and keeping the forearm vertical throughout the movement.
Coaching tip: Start with a light kettlebell in a strong bottoms-up rack position. Brace your core, engage your grip, and press straight up with control. Lock out fully and reverse the motion smoothly back to the start.
The kettlebell bottoms-up press builds shoulder integrity, neuromuscular coordination, and functional upper-body strength. It’s ideal for warm-ups, rehab, or advanced skill-focused strength work.
Learn more: Develop bulletproof shoulders with the kettlebell bottoms-up press.
Kettlebell Farmers Carry

The kettlebell farmer’s carry is a foundational carry exercise that builds full-body strength, grip endurance, and core stability. Simply walking while holding heavy kettlebells at your sides trains your body to stay braced and aligned under load.
This movement targets the forearms, traps, lats, core, glutes, and legs. It strengthens your posture, improves breathing mechanics under tension, and enhances real-world strength for lifting and carrying tasks.
Common mistakes include rounding the shoulders, leaning to one side, or letting the kettlebells swing. Keep your spine tall, shoulders pulled back, and steps steady and controlled.
Coaching tip: Choose a pair of kettlebells that challenge your grip but allow for good posture. Walk in a straight line with your eyes forward, breathing under tension and maintaining full-body tension from start to finish.
The kettlebell farmer’s carry builds loaded carry capacity, core integrity, and overall resilience. It’s perfect for finishers, grip work, or integrating into strength circuits for real-life performance gains.
Kettlebell Sit and Press

The kettlebell sit and press is a full-body movement that combines core strength, hip mobility, and overhead pressing in one fluid sequence. It challenges your ability to transition from the floor to a seated position and press the kettlebell overhead with control.
This exercise targets the abs, hip flexors, shoulders, triceps, and obliques. The sit-up motion builds trunk stability, while the overhead press reinforces posture, shoulder strength, and upper-body alignment.
Common mistakes include collapsing the spine during the sit-up, pressing with poor alignment, or rushing through the movement. Keep your spine long, core tight, and press only when fully upright.
Coaching tip: Start lying on your back with the kettlebell in one hand, arm extended. Sit up under control, maintaining a vertical forearm. Once seated, press the bell straight overhead, then reverse the motion back to the floor.
The kettlebell sit and press develops core-to-shoulder connection, overhead control, and functional strength. It’s great for warm-ups, skill-focused core work, or combining strength with mobility in your training routine.
Kettlebell Windmill
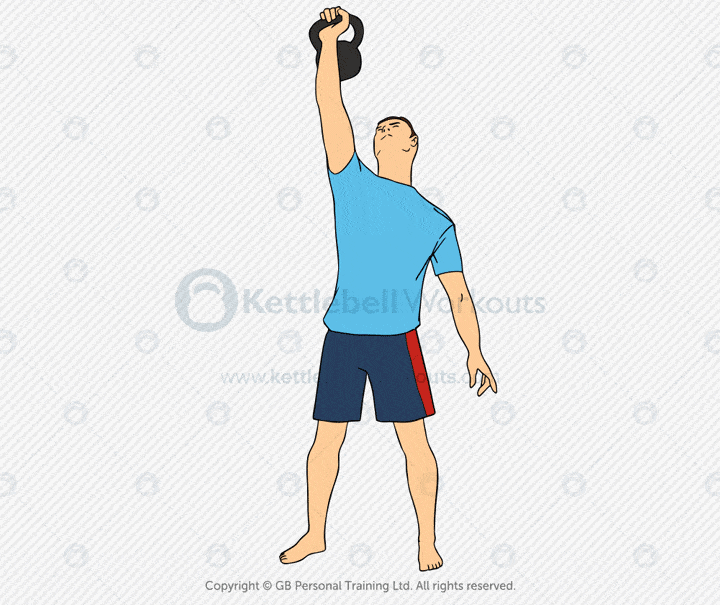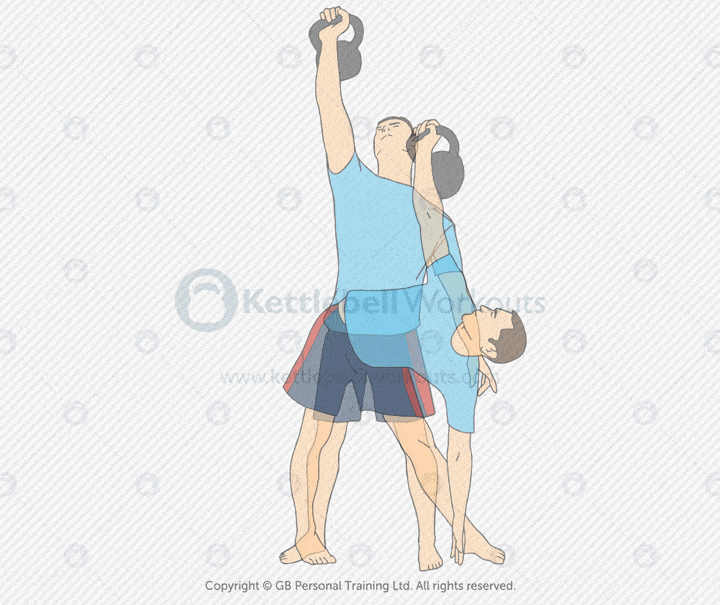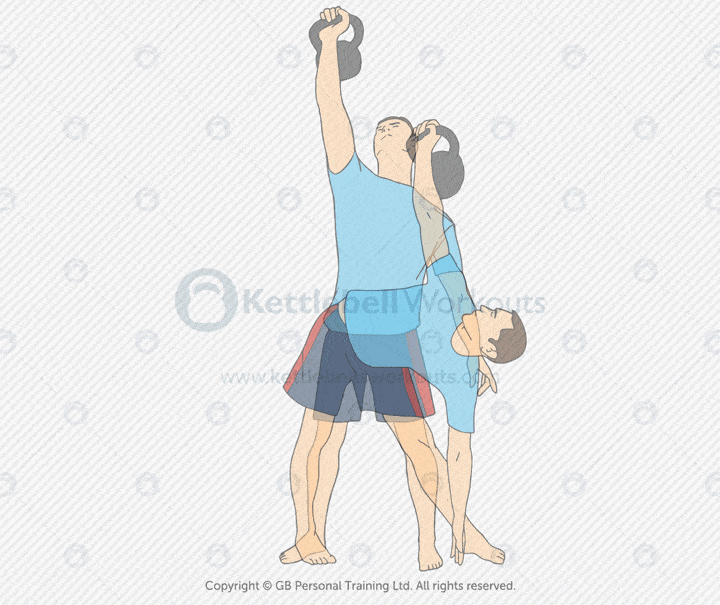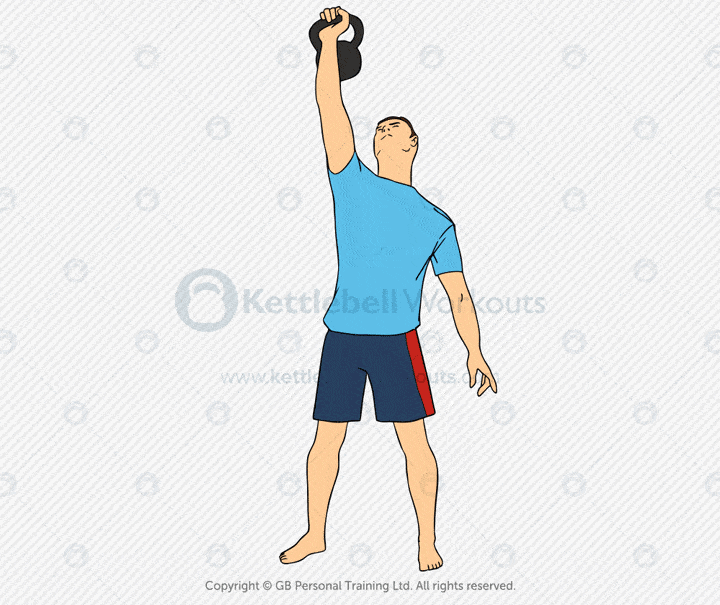
The kettlebell windmill is a dynamic mobility and strength exercise that builds shoulder stability, core control, and hip mobility. It involves rotating through the hips while keeping a kettlebell locked overhead, challenging multiple planes of movement.
This exercise targets the obliques, glutes, hamstrings, lats, and delts. It also stretches the hip flexors, hamstrings, and thoracic spine, making it excellent for mobility and stability training.
Common mistakes include bending the front knee, losing the overhead lockout, or twisting through the lower back. Keep your legs mostly straight, hips pushed back, and your eyes on the kettlebell at all times.
Coaching tip: Start with the kettlebell in the overhead position on one side. Turn your feet at a slight angle, push your hips back, and lower your torso while keeping the bell vertical. Touch the floor or your shin with the opposite hand, then return to standing.
The kettlebell windmill builds rotational stability, joint mobility, and functional strength. It’s ideal for improving movement quality, prepping for overhead lifts, or integrating into mobility-focused sessions.
Kettlebell Turkish Get Up

The kettlebell Turkish get-up is a foundational full-body movement that builds mobility, stability, and total-body strength. It involves transitioning from lying on your back to standing up—while holding a kettlebell locked out overhead the entire time.
This exercise targets the shoulders, core, glutes, hips, triceps, and obliques. It improves joint stability, body awareness, and motor control, making it one of the most functional exercises in kettlebell training.
Common mistakes include rushing the movement, losing tension, or bending the elbow overhead. Each phase should be deliberate and precise. Keep your eyes on the kettlebell, your arm vertical, and your body under control at all times.
Coaching tip: Break the movement into steps—roll to elbow, post to hand, bridge, sweep the leg, lunge up, then stand tall. Reverse the steps to return to the floor. Use a light kettlebell until the pattern is clean and consistent.
The kettlebell Turkish get-up builds resilience, overhead stability, and full-body coordination. It’s essential for building movement efficiency and injury-resistant strength, and should be a staple in any well-rounded kettlebell program.
Kettlebell Hip Thrust

A core intensive kettlebell exercise that will help to mobilise the upper back and thoracic spine at the same time. Perform slowly with control and using the proper technique.
Kettlebell Reverse Turkish Get Up

The kettlebell reverse Turkish get-up is a high-skill movement that builds full-body control, shoulder stability, and core strength by reversing the traditional get-up pattern. Instead of standing up with the kettlebell, you start at the top and lower yourself to the ground step-by-step.
This exercise targets the shoulders, obliques, glutes, hamstrings, and triceps. The reverse flow helps improve motor control, body awareness, and movement precision, especially for lifters refining their Turkish get-up technique.
Common mistakes include rushing transitions, losing tension, or letting the kettlebell drift out of alignment. Maintain focus, keep your eyes on the bell, and move slowly through each position with deliberate control.
Coaching tip: Start in a full standing position with the kettlebell overhead. Step back into a lunge, then carefully lower to the floor through the kneeling, bridging, and seated phases. Maintain full-body tension and overhead alignment throughout.
The kettlebell reverse Turkish get-up is excellent for improving shoulder stability, mobility, and technical consistency. Use it as a warm-up, skill drill, or mobility-focused session to sharpen movement awareness and control.
Kettlebell Deck Squat

The kettlebell deck squat is a dynamic, ground-to-stand movement that builds hip mobility, leg strength, and explosive coordination. It involves rolling back onto the floor with control and then driving forward into a standing squat while holding a kettlebell.
This exercise targets the quads, glutes, hamstrings, core, and hip flexors. It also improves body control, spinal awareness, and transitional power—key qualities for athletic performance and functional movement.
Common mistakes include flopping to the ground, relying on momentum, or losing kettlebell control during the rise. Stay tight through the core, control the roll, and use the legs—not the arms—to power back to standing.
Coaching tip: Hold the kettlebell in a goblet position. Lower into a deep squat and roll gently onto your back, keeping the bell close. Tuck your feet under and explode forward into a standing position, finishing in a tall, balanced stance.
The kettlebell deck squat builds fluid strength, mobility, and real-world movement efficiency. It’s perfect for warm-ups, mobility-focused circuits, or bodyweight skill sessions enhanced with load.
- What are the best kettlebell exercises?Your goals will determine which kettlebell exercises are right for you. The kettlebell swing, Turkish get up, goblet squat and the clean and press are some of the most popular.
- Do kettlebell exercises really work?Kettlebell training can activate hundreds of muscles per movement, improve your cardio and strengthen your entire body, all without you even moving your feet.
- How many days a week should you use kettlebells?Everybody recovers from exercise differently but usually 3 – 5 workouts per week is about right for most people. The more intense the workouts the more rest days you will need.
